4

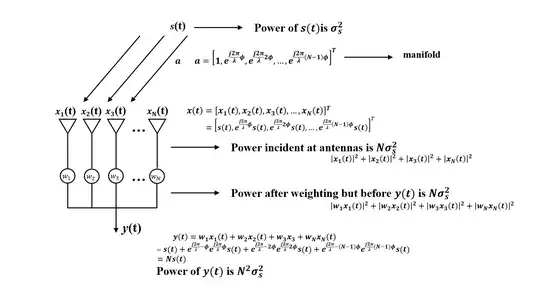
Consider a normal array model with $N$ element. The output of the array is given by,

$$\mathbf{y}=\mathbf{w}^H\mathbf{x}=\mathbf{w}^H\mathbf{as}$$

where

  • $\mathbf{a}=[a_1,...,a_N]^T=\in\mathbb{C}^{N\times 1}$ is the manifold of the desired signal (I ignore the noise for simplicity).

    • $T$ denotes the transpose.

  • $\mathbf{s}\in\mathbb{C}^{1\times M}$ is the desired signal

    • $M$ is the number of snapshots and
    • the power of $\mathbf s$ is $\sigma_s^2=\operatorname E(|\mathbf{s}(t)|^2)=\operatorname E(\mathbf{ss}^H)=\frac{1}{M}(|\mathbf{s}(1)|^2+...+|\mathbf{s}(M)|^2), \mathbf{ss}^H=|\mathbf{s}(1)|^2+...+|\mathbf{s}(M)|^2$
    • $t$ is the time index,

  • $\mathbf{x}\in\mathbb{C}^{N\times M}$ is the desired signal incident at each antenna, $\mathbf{x}(t)=[\mathbf{x_1}(t),...,\mathbf{x_N}(t)]^T=[a_1\mathbf{s}(t),...,a_N\mathbf{s}(t)]^T$

  • $\mathbf{w}\in\mathbb{C}^{N\times 1}$ is the receiving weight (where $\mathbf w = \mathbf a$),

  • $^H $ denotes the conjugate transpose and

  • $\operatorname E$ denotes the expectation.

Therefore the power of the output $y$ is given by, $$P_y=\operatorname E (|\mathbf{y}(t)|^2)=\frac{1}{M}(|\mathbf{y}(1)|^2+...+|\mathbf{y}(M)|^2)=\frac{1}{T}(\mathbf{y} \mathbf{y}^H)=\frac{1}{T}(\mathbf{a}^H\mathbf{ass}^H\mathbf{a}^H\mathbf{a})=\sigma_s^2(\mathbf{a}^H\mathbf{a}\mathbf{a}^H\mathbf{a})=\sigma_s^2(N\times N)=N^2\sigma_s^2$$

I think the power of the desired signal that incident at the receiving array is, $$P_{inc}=P_{x_1}+...+P_{x_N}=\operatorname E(|\mathbf{x_1}(t)|^2)+...+\operatorname E(|\mathbf{x_N}(t)|^2)=\frac{1}{M}(|\mathbf{x_1}(1)|^2+...+|\mathbf{x_1}(M)|^2)+...+\frac{1}{M}(|\mathbf{x_N}(1)|^2+...+|\mathbf{x_N}(M)|^2)=\frac{1}{M}a_1\mathbf{s}(a_1\mathbf{s})^H+...+\frac{1}{M}a_N\mathbf{s}(a_N\mathbf{s})^H=\sigma_s^2a_1a_1^H+...+\sigma_s^2a_Na_N^H=N\sigma_s^2$$

($\operatorname{tr}(\mathbf A)$ denotes the trace of $\mathbf A$)

then the beamforming brings gain of $N$ to the power of the received desired signal.

What confuse me is why the total power of desired signal is changed. According to my understanding, the power should remain unchanged as the signal power incident at the array is certain and beamforming won't add power to it.

I think I was wrong but I don't know where. Is it related to the concept of effective array and directivity gain? Am I calculating the desired signal power that incident at the array before beamforming right?

I add the figure below to help me explain my problem. My question can be summarized as why the received signal power after beamforming (which is power of $y(t)$) is $N$ times of signal power of incident signal power or signal power before adding up? Is there a physical explanation for this?

enter image description here

tyrela
  • 145
  • 6
  • 1
    Not sure I can follow this. What are "snapshots"? What's $E$? What's $H$? – Phil Frost - W8II Jul 25 '21 at 14:40
  • Sorry I didn't give specific definition at last edit. $E$ denotes the mathematical expectation and $H$ denotes conjugate transpose. – tyrela Jul 26 '21 at 02:00
  • And $t$? $r$? I guess you're doing some kind of least-mean-squares dynamic weighting? Please provide some context, it's impossible to check your math otherwise. – Phil Frost - W8II Jul 26 '21 at 14:19
  • I am very sorry! $tr$ denotes the trace of matrix of $(aa^H)$. I add a picture in my question. I hope it can help me to explain my problem. – tyrela Jul 27 '21 at 02:55
  • I don't see the picture, but maybe some tweaks to the notation might make it a little easier to grok. Something like the trace can use `\operatorname{tr}`, that formats it in a different font so it doesn't look like variables. And you can use `\mathbf` to make letters bold to indicate they are matrices, like $\operatorname{tr}(\mathbf{A})$ – Phil Frost - W8II Jul 27 '21 at 03:20
  • 1
    Really thanks! I will do some edits on that! I have uploaded the picture and I hope it helps to explain my problem. – tyrela Jul 27 '21 at 03:24
  • 1
    Very helpful, thanks for taking the time to clarify the question! – Phil Frost - W8II Jul 27 '21 at 03:34
  • in the text it looks like you're treating $\mathbf y$ as a matrix, but in the picture $y$ is the sum of the products of the signals and their weights, and so is a scalar, right? – Phil Frost - W8II Jul 27 '21 at 03:49
  • In the text, $\mathbf{y}$ is the signal with $T$ snapshots, so yes it's a vector or matrix. In the picture, $y$ or $y(t)$ is the signal at the time index $t$, so it's a scalar. But basically it's the same thing. – tyrela Jul 27 '21 at 03:58
  • I've changed $w=a$ to $\mathbf w = \mathbf a^H$, hope that's correct. – Phil Frost - W8II Jul 27 '21 at 13:33
  • Perhaps you can explain what this $\operatorname E$ does more specifically? Best I can tell from some cursory research, the expected value of a matrix is a matrix of the same dimensions, simply the expected value of each element in the matrix. Which, if there's no noise in your example, makes $\operatorname E$ an identity operator, and $\sigma^2_s \in \mathbb C^{T \times T}$, which I don't know how to interpret as power. – Phil Frost - W8II Jul 27 '21 at 13:43
  • Another contradiction, I think: you state $\mathbf w \in \mathbb C^{1\times N}$ and $\mathbf a \in \mathbb C^{N\times 1}$ so these matrices are compatible, which is why I changed it to $\mathbf w = \mathbf a^H$. But then you multiply $\mathbf w^H \mathbf a$ as part of $\mathbf y$, which is not compatible. – Phil Frost - W8II Jul 27 '21 at 13:59
  • Actually, $\mathbf{w}=\mathbf{a}\in \mathbb{C}^{N\times1}$ doesn't need to be changed. The weight is used to compensate the phase difference on each antenna. So in this case, the weight can be simply set as the conjugate of $\mathbf{a}$(manifold). Then, after weighting, $N$ signals from each receiving chain adds up as $\mathbf{y}$. Therefore, we take transpose of conjugate of $w$ to further express the process of "add up". Now we can write this process in matrix eqautions as $\mathbf{w}^H\mathbf{as}=\mathbf{y}$. The dimension now goes like $(1\times N)\times (N\times1)\times(1\times T) $ – tyrela Jul 27 '21 at 14:10
  • For $w\in \mathbb{C}^{1\times N}$, it's my mistake! Very sorry! It should be $w=a\in \mathbb{C}^{N\times 1}$! – tyrela Jul 27 '21 at 14:18
  • As for $\mathbf{E}$, for finite signal, it's basically the process of average over time. I rewrite the computation of $P_{inc}$ and $P_y$. Please check it. – tyrela Jul 27 '21 at 14:22
  • Please define what you mean by $\operatorname E$ rigorously, if you'd like a check on your math. You seem to be defining the expected value of a matrix in some way which is different from [the](https://en.wikipedia.org/wiki/Expected_value#General_case) [typical](http://www.utstat.toronto.edu/~brunner/oldclass/appliedf11/handouts/2101f11RandomVectorsMVN.pdf) [way](https://math.stackexchange.com/a/644423/139015). – Phil Frost - W8II Jul 27 '21 at 14:35
  • $\mathbf{E}$ is mean or average to compute the average power. For example $\mathbf E(\mathbf{ss}^H)=\frac{1}{N}(|s(1)|^2+|s(2)|^2+...|s(N)|^2)$ – tyrela Jul 27 '21 at 14:53
  • In this case $\mathbf{E}(a)=\mathbf{a}$, as $\mathbf{a}$ is a constant matrix or vector. Its element is constant not variable. – tyrela Jul 27 '21 at 14:57
  • Or it's like $\mathbf{E} (|\mathbf{s}(t)|^2)=\frac{1}{N}(|\mathbf{s}(1)|^2+...+|\mathbf{s}(N)|^2)=\mathbf{E} (\mathbf{s} \mathbf{s}^H)$ – tyrela Jul 27 '21 at 15:08
  • $|\mathbf{s}(t)|^2$ denotes the instantaneous power of $\mathbf{s}$, so $\mathbf{E} (|\mathbf{s}(t)|^2)$ is the expectation of $|\mathbf{s}(t)|^2$, which is the average power. And it can be formulated as $\mathbf{E} (\mathbf{ss}^H)$. – tyrela Jul 27 '21 at 15:14
  • Edit the question please -- it's like a mod is going to delete all these comments – Phil Frost - W8II Jul 27 '21 at 17:24
  • OK, I will edit! – tyrela Jul 28 '21 at 02:11
  • Now you've introduced $\mathbf t$ without defining it, though the formatting suggests it could be a matrix. And several of the values such as $\mathbf s$ are now sometimes used as functions, but sometimes not. I'm guessing t is time, and sometimes you are representing signals as matrices where one of the dimensions is time, and other times signals are functions of time. Please, pick a notation, explain it, and stick to it consistently! – Phil Frost - W8II Jul 28 '21 at 12:44
  • 1
    I was really sorry for my mistakes. I have edited it. $t$ is the time index. For example, $\mathbf{x}(t)$ is just one column of matrix $\mathbf{x}$, which is ranged from 1 to $T$. Is this clear to you? For signal average power, mathematically, it's the expectation of the instantenous power, so it can be formulated as $\sigma_s^2=\mathbf{E} (|\mathbf{s}(t)|^2)$. And for a finte signal with $T$ snapshots, it can be further calculated as the time average, which is $\sigma_s^2=\mathbf{E} (|\mathbf{s}(t)|^2)=\frac{1}{M}(|\mathbf{s}(1)|^2+...+|\mathbf{s}(M)|^2)$ – tyrela Jul 28 '21 at 13:23
  • And $\mathbf{ss}^H=|\mathbf{s}(1)|^2+...+|\mathbf{s}(M)|^2$, this is just the matrix form and the detailed computational process, which is absolutely right. – tyrela Jul 28 '21 at 13:44
  • Comments are usually deleted (and moved to a new chat room) when they get chatty and don't conform to our [commenting guidelines](https://ham.stackexchange.com/help/privileges/comment). Any comments that have served their purpose (and were added to the question) should probably be. – Mike Waters Jul 31 '21 at 11:44
  • @tyrela Having said that, kindly move your last comment (which explain your $\mathbf{ss}^H$ variable) to your question, where it need to be. Comments are not searchable, and people should not have to read comments to understand the question. – Mike Waters Jul 31 '21 at 11:52
  • 1
    Thanks for the remind. I will edit it. – tyrela Aug 01 '21 at 01:55

2 Answers2

3

I don't understand the parameters of your equations.

But ignoring the equations and answering the text of the question: beam forming depends on frequency and phase. If the phase of the output of two beam forming elements is equal in magnitude but opposite in phase at the angles and frequency of measurement, the received output power output from that 2 element array is zero. If the phase and power are the same, the output power can be doubled. etc.

Antenna directivity is associated with a (spherical) angle of EM wave incidence and frequency. The number of elements can affect an antenna's effective aperture size. But that's also angle and frequency dependent.

hotpaw2
  • 13,116
  • 6
  • 40
  • 72
  • I think my problem can be summarized as whether the total signal power incident at the array equals the power after beamforming (when output power and phase are the same)? – tyrela Jul 26 '21 at 02:23
  • Beam forming itself won't increase the total power, but the resulting aperture increase might, because it increases the surface area the energy can be incident upon. Energy that might have otherwise passed the antenna without touching it can be absorbed. – user10489 Jul 27 '21 at 11:23
  • Then, when signal arrives at the array but before the beamforming, how much power? – tyrela Jul 27 '21 at 15:48
  • With or without the aperture change? From one direction or from all directions? – user10489 Jul 28 '21 at 12:14
  • Just one desired signal from far field, incident at a $N$ element half wave length spaced linear array, and the receive weight is the transpose conjugate of the manifold of the angle-of-arrival of the desired signal. So the total signal power before and after the beamforming, what's the difference? – tyrela Jul 28 '21 at 13:27
  • There may be no "before" beamforming (unless you remove elements, and measure them individually). The elements interact in some nulls to re-radiate power, and thus never receive power in a measurable form. – hotpaw2 Jul 28 '21 at 15:49
2

Since the originating signal is not a unidimensional, laser-like effect, but rather an inverse-square-law wave... an enormous percentage of the original signal is neglected by a single element antenna system and a minuscule percentage is captured.

Adding additional elements does not increase the power of the transmitted signal, rather the amount of RF neglected by the array is decreased.

When your reference power is what is transferred to a single element (instead of the transmitted power), then you have positive gain.

webmarc
  • 3,605
  • 1
  • 17
  • 40