Wavepropagation through air - EMC test values 100V/m

Question

I am reading the Automotive International standards ISO 11452 and it states that I must have a chamber in which I must generate 100V/m on a range of frequency.

My question is: In which circumstances around the world do I get in the air over 100V/m?

For example the GSM in Europe is between 880-915MHz and I am curious when is my driving car "bombarded" with electromagnetic energy with over 100V/m over that frequency range?

Answer 1

Field strength in the far field is $E = 5.477 \frac{\sqrt{P}}{r}$. If P is watts and r is meters, then E is V/m.

So 100 V/m is approximately the field strength of

• 100 W at half a meter
• 1000 W at 1.7 meters
• 10 kW at 5.5 meters

etc. as long as the frequency is high enough to make those distances significantly more than a wavelength. If that's not true, you're in the near-field, and so the electric field strength could be higher (or, then again, it could be lower, depending on the radiator and the exact distance).

Answer 2

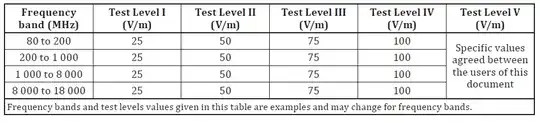
The test severity level is something that will be requested, or specified, between the purchaser and the supplier. In other words you don't just "comply to ISO 11452", you will have a requirement for conducted and radiated susceptibility to be at severity level 3 for some frequency band, and 2 for others, etc. I can't quickly find out what would typically be expected or required by national law etc, but it's probably not the maximum.

A normal cellular phone will generate more than 30 V/m near the device.

If you were around for the arrival of phones in the 1990s, you'll remember all the electromagnetic compatibility issues then. Radios and alarm clocks buzzing. My PDA would be scrambled by a phone near it. I discovered that my phone would unlock the office door keycard system from the outside. In an underground parking lot, my 50 watt ham radio would reliably trigger the alarms in parked cars. And in an EMC chamber once I found a "one arm bandit" slot machine being tested, they obviously have very good reasons to want to be immune to RF interference.

These issues have largely been solved now, driven by these improved standards, so you don't hear the buzz in audio devices, and you don't expect computers and gadgets to be scrambled by your phone. You're allowed to use your phone on an aeroplane.

Back to the vehicle: handheld radios, up to 8 watts, could generate nearly 100 V/m near the radio. Worse, a vehicle-mounted 80 watt transceiver, with its RF connection partially undone so only the centre pin makes contact, would generate much more, right under the dashboard. Consider that these tests are for safety systems like the airbags, not just the audio amplifiers, and 100 V/m sounds like a reasonable level.

As a quick calculation: for a TEM (far field) wave, $ P_d = {E^2\over{377}}$ so 100 V/m is a power density of 26 watts per square metre. 80 watts would achieve 100 V/m inside a sphere of about 1 metre diameter.

The field strength from the cellphone towers and other external sources will be much, much smaller, less than 1 V/m.

Answer 3

In terms of power density, a signal traveling with a field strength of $E_0$ V/m will have an average power density of $$\left<S_i\right> = \frac{E_0^2}{2\eta_0}$$ where $\eta_0$ is the characteristic impedance of free space: $$\eta_0 = \sqrt{\frac{\mu_0}{\epsilon_0}} \approx 376.73\Omega$$

---

At Test Level IV $$\left<S_i\right> = \frac{100^2 \text{V}^2/\text{m}^2}{2\cdot376.73\Omega} \approx 13.3 \text{W}/\text{m}^2 $$

Is this a realistic ambient power level?

The output power density due to a radiator with $P_T$ watts input to an antenna with gain $G$ as a function of range, $r$, will be in free space: $$\left<S_i\right> = G \frac{P_T}{4\pi r^2}$$

The legal maximum output power of a WiFi transmitter at 5 GHz is 4 W. WiFi antennas typically have antenna gains in the range of 2-4 dBi (dB over an isotropic equivalent). Plugging 2 in for $G$ ($\approx 3$ dBi) and 4 in for $P_T$ we get: $$\frac{2\cdot4\text{W}}{4\pi r^2} = 13.3 \text{W}/\text{m}^2 \rightarrow r=\sqrt{\frac{8}{4\pi\cdot 13.3}}\text{m} \approx 0.05 \text{m or } 5\text{ cm}$$

So a scenario here might be an internal WiFi hotspot in a car to deliver internet to passengers that could be close to some automotive component. So the scenarios aren't completely unrealistic.

---

^{General formula for field strength at a given distance from an emitter (free space model): $$ \frac{E_0^2}{2\eta_0} = G \frac{P_T}{4\pi r^2} \rightarrow E_0 = \sqrt{2\eta_0\cdot G \frac{P_T}{4\pi r^2}} = \frac{1}{r}\sqrt{\frac{\eta_0GP_T}{2\pi}} $$}