What decimal precision does Excel support?

Question

What precision does Excel support? I tried to calculate 0.800000000000001 / 2 and received incorrect result of 0.40000000000000000000, where it should be 0.4000000000000005

Answer 1

Excel supports Floating Point arithmetic, which has a limit of 15 decimal places. Here is the investigation and reference.

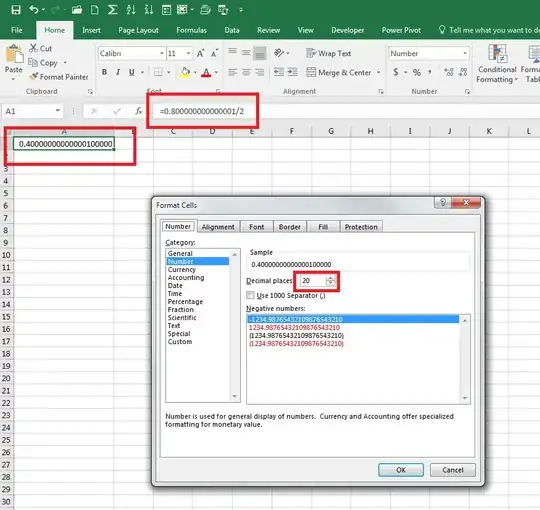
In researching this subject, it is found that only 15 digits are stored in arithmetic quantities, due to Floating Point Notation as suspected.

After searching for this suspected culprit, the reference is found here: https://support.microsoft.com/en-us/kb/78113 and here https://support.microsoft.com/en-us/kb/214118

So, 15 decimal places is the maximum carry over in floating point. Here is the same example in 14 decimal places. Note the 5 in the 14th decimal place; presents further demonstration of the Floating Point limits.

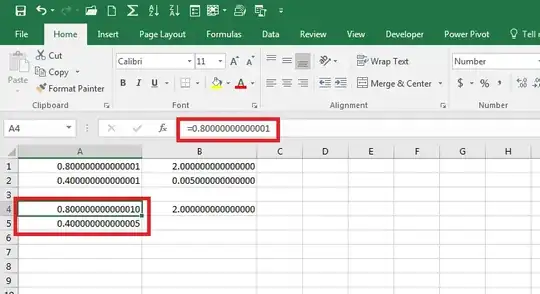
To test a theory, commented by a member in this forum, I decided to add this addendum. No, not even in VBa can the Double variable surpass the Floating Point limitations. I used Double precision and returned the value as String to demonstrate even further here:

An Exception to the Rule!

Thank you, Ron Rosenfeld. With regards to the last image, regarding VBa. If you are using VBa code, then utilizing the VBa library function CDec() does indeed capture the precision not covered in the limits as discussed above. However, with one caveat, you must return the data as a String for display purposes. A reference can be found here: http://www.techonthenet.com/excel/formulas/cdec.php

Answer 2

Here is an example of how to use the VBA Decimal data type in simple math operations, to obtain higher precision than Excel's 15 decimal digit precision.

Obviously, you can expand this to use for other types of operations. However, if 28 decimal precision, or if the allowable number range (see Help) is not sufficient, you will need a different tool.

The below example is only for Addition, Multiplication and Division. But you can easily extend it to other operations, or implement it differently, according to what you really need.

Note that the results are returned as a string (text). Otherwise Excel will not be able to display the results. If you were using it solely within VBA, you could return the result as a Variant/Decimal.

Function HiPrecMath(sOp As String, ParamArray Factors() As Variant) As String
    Dim V As Variant
        V = Factors
    If sOp Like "Add*" Then
        HiPrecMath = vbADD(V)
    ElseIf sOp Like "Mult*" Or sOp Like "Prod*" Then
        HiPrecMath = vbMULT(V)
    ElseIf sOp Like "Div*" Then
        HiPrecMath = vbDIV(V)
    End If
End Function

Private Function vbADD(F) As String
    Dim vRes As Variant
    For I = 0 To UBound(F)
        vRes = vRes + CDec(F(I))
    Next I
vbADD = vRes
End Function

Private Function vbMULT(F) As String
    Dim vRes As Variant
    vRes = F(0)
    For I = 1 To UBound(F)
        vRes = vRes * CDec(F(I))
    Next I
vbMULT = vRes
End Function

Private Function vbDIV(F) As String
    Dim vRes As Variant
    vRes = F(0)
    For I = 1 To UBound(F)
        vRes = vRes / CDec(F(I))
    Next I
vbDIV = vRes
End Function

Here is an example using your data: