-3

Why is it that Microsoft Excel 7 says that 8^(-1^(-8^7))) = 8 while Wolfram Alpha says it equals 1/8?
These results are the same if I substitute -2097152.0 for -8^7.
Now -1 to any power is -1. Therefore -1^(-8^7) = -1. And 8^-1=1/8.
Excel is wrong.
Try it and see!

Geezer
  • 15
  • Excel 7 is 20 years old, there have been hundreds of bugs, this likely was one of them. Stop using software from 1997. – Ramhound Aug 29 '16 at 22:21
  • 1
    I'm voting to close this question as off-topic because Excel 7 (Excel 97) is from 1997, there is no possible way, for anyone to know the reason Excel 97 incorrectly calculated the specified value – Ramhound Aug 29 '16 at 22:23
  • @Ramhound He's also wrong in the first place. 8^((-1)^(-8^7)) is not the same as 8^(-1^(-8^7)) to Wolfram. It is to excel; in fact, Excel is more refined than Wolfram with this calculation. – var firstName Aug 29 '16 at 22:23
  • 3
    I'm voting to close this question as off-topic because `8^(-1^(-8^7)))` has mismatched parentheses and is therefore an invalid expression. – DavidPostill Aug 29 '16 at 22:43
  • Just clarification for potential close voters: 1) A question is not off-topic because it is about old software; that just limits how many people can answer (and this problem is not limited to Excel 7). 2) A question is not necessarily off-topic because of mismatched parentheses; that might be the answer. 3) Questions that exist only because of a typo are generally considered off-topic because they aren't really about a hardware or software problem. That appears to be the case here. Rather than create a 3rd custom close reason, DavidPostill's reason is close enough for government work. – fixer1234 Aug 29 '16 at 23:48
  • 1
    It turns out this has nothing to do with Excel 97. Can be replicated in Excel 20013/2016. See `=8^(-1^(-8^7))` = 8 vs `=8^(-(1^(-(8^7))))` = 0.125 – Brad Aug 29 '16 at 23:57
  • @fixer1234 I've deleted my comment. – DavidPostill Aug 31 '16 at 06:45
  • [Why does =-x^2+x for x=3 in Excel result in 12 instead of -6?](https://superuser.com/q/1385570/241386), [According to Excel, 4^3^2 = (4^3)^2. Is this really the standard mathematical convention for the order of exponentiation?](https://superuser.com/q/1386517/241386) – phuclv Apr 16 '20 at 16:08

4 Answers4

3

Excel and Wolfram Alpha have difference precedence rules for parsing an expression like this involving exponentiation and unary minus.

- x ^ y

Excel treats unary minus as higher precedence and does it first, evaluating the expression as:

( - x ) ^ y

Wolfram Alpha does the exponentiation first, evaluating the expression as:

- ( x ^ y )
Nicole Hamilton
  • 9,935
  • 1
  • 21
  • 43
2

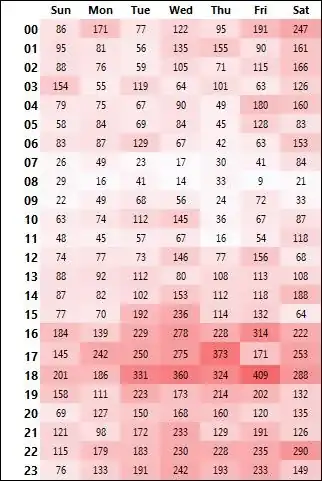
The problem is that in Excel the minus sign is used to signify both the subtraction operator and the unary sign. It is easy to illustrate this. In A1 enter:

=-1^(ROW())

and copy down:

enter image description here

The flip/flopping positive/negative indicates that Excel sees the minus sign as a unary and treats this formula like:

=(-1)^(ROW())

Now in B1 enter:

=0-1^(-ROW())

and copy down:

enter image description here

The lack of flip/flopping indicates that Excel sees the minus sign as a subtraction operator and treats this formula like:

=0-(1^(-ROW()))

Of course, the user can always control the precedence by using parenthesis.

EDIT#1:

See Bill Jelen's explanation

Gary's Student
  • 19,266
  • 6
  • 25
  • 39
1

Wolfram Alpha does this:

-(1-2097152) = -(1) = -1

8-1 = 1/8

Excel, on the other hand, does this:

(-1)-2097152 = 1

81 = 8

Indeed, Excel is wrong - it should exponentiate first, then negate. Try this formula: =8^(-(1^(-8^7)))

Now -1 to any power is -1

As var firstName already pointed out, that's incorrect. However, it's true that -1N = -1 is true for any N - again, because you should exponentiate first, then negate.

Community
  • 1
gronostaj
  • 55,965
  • 20
  • 120
  • 179
  • No, actually, Excel is right. That method of entry is incorrect. OP meant 8^((-1)^((-8)^7)) – var firstName Aug 29 '16 at 22:26
  • @varfirstName Why would it be incorrect? Standard [order of operations](https://en.wikipedia.org/wiki/Order_of_operations) is: exponents and roots, then multiplication and division, then addition and subtraction. So basically the Wolfram Alpha order. Excel groups (-1) first (basically `0 - 1` subtraction), then exponentiates - that's incorrect order. – gronostaj Aug 29 '16 at 22:30
  • if the post-calculation multiplication was intended, it would be marked by extra separating parentheses. – var firstName Aug 29 '16 at 22:34
  • @varfirstName "OP meant 8^((-1)^((-8)^7))". You don't know that. It's not what he wrote (in two different places). – DavidPostill Aug 29 '16 at 22:46
  • @gronostaj I think more properly stated is that Excel ranks **negation** first (unary minus), and then `exponentiation`, then `multiplication and division`, then `addition and subtraction`. In Excel, `-1` is different from `0-1`. eg: `-1^2` ► `1`. `0-1^2` ► `-1`. The first is considered a unary operator, the second a binary operator. – Ron Rosenfeld Aug 31 '16 at 12:25
0

That's incorrect. -1^2 is 1. However, -1 to any odd power is -1; that is true. Using perfectly sensible logic, you can say that 8^(-1^(-8^7)). -8 ^ 7 = -2,097,152, an even number; therefore, -1^(-2,097,152) is 1/(-1^(2,097,152)) which reduces to 1/1 or simply 1, and 8^1 is 8. Your entry to WolframAlpha is flawed in some way.

EDIT: I did the calculation on Wolfram and it turns out that you entered it wrong. You're supposed to isolate the -1 further from the base, like this: 

8^( (-1)^(-8^7) )

Wolfram spit this out back at me (identical to my entry):

8^((-1)^(-8^7))
var firstName
  • 1,777
  • 10
  • 18
  • 1
    He says that -1 to *any* power is -1 which is completely incorrect. – var firstName Aug 29 '16 at 22:30
  • No, that's completely incorrect, any number to the -1 is 1 over that number – var firstName Aug 29 '16 at 22:32
  • My point is, he said *negative one* to **_any_** power is -1, which is incorrect. (negative one being the base, in all circumstances.) – var firstName Aug 29 '16 at 22:36
  • Let us [continue this discussion in chat](http://chat.stackexchange.com/rooms/44656/discussion-between-var-firstname-and-ramhound). – var firstName Aug 29 '16 at 22:39
  • This is wrong. In math power operator has higher precedence than unary minus so [-1^2 = -1](https://en.wikipedia.org/wiki/Order_of_operations#Unary_minus_sign), and it has right-to-left associativity so [2^3^4 = 2^(3^4)](https://en.wikipedia.org/wiki/Order_of_operations#Serial_exponentiation). Almost all languages with power operator do follow the math rule like that. See [Why is exponentiation applied right to left?](https://stackoverflow.com/q/47429513/995714), [Why is exponentiation right associative?](https://math.stackexchange.com/q/1673740/90333) – phuclv Apr 16 '20 at 16:08